MATEMATICAS. GRADO 7-1. TEMA: REPRESENTACIÓN EN LA RECTA NUMÉRICA

 INSTITUCIÓN EDUCATIVA ALFREDO BONILLA MONTAÑO

MATEMÁTICAS. PRIMER PERIODO. GRADO 7-1

TEMA: REPRESENTACIÓN EN LA RECTA NUMÉRICA

LICENCIADA:  DIXI SUAREZ B  

  

  DEFINICIÓN DE NÚMEROS ENTEROS:

 Los números positivos, negativos y el cero forman el conjunto de los números enteros.

Positivos:  +1, +2, +3, +4, +5, +6, … (naturales con signo +)

Negativos:  -1, -2, -3, -4, -5, …. (naturales con signo -)

Cero: 0 es Neutro.

 Números enteros (Z): Recta Numérica

Representación:

Para representar los número enteros se utiliza una recta numérica.

Los números positivos a medida que se alejan del CERO (0) son más grandes o mayores.

Los números negativos a medida que se alejan del CERO (0) son más pequeños o menores.

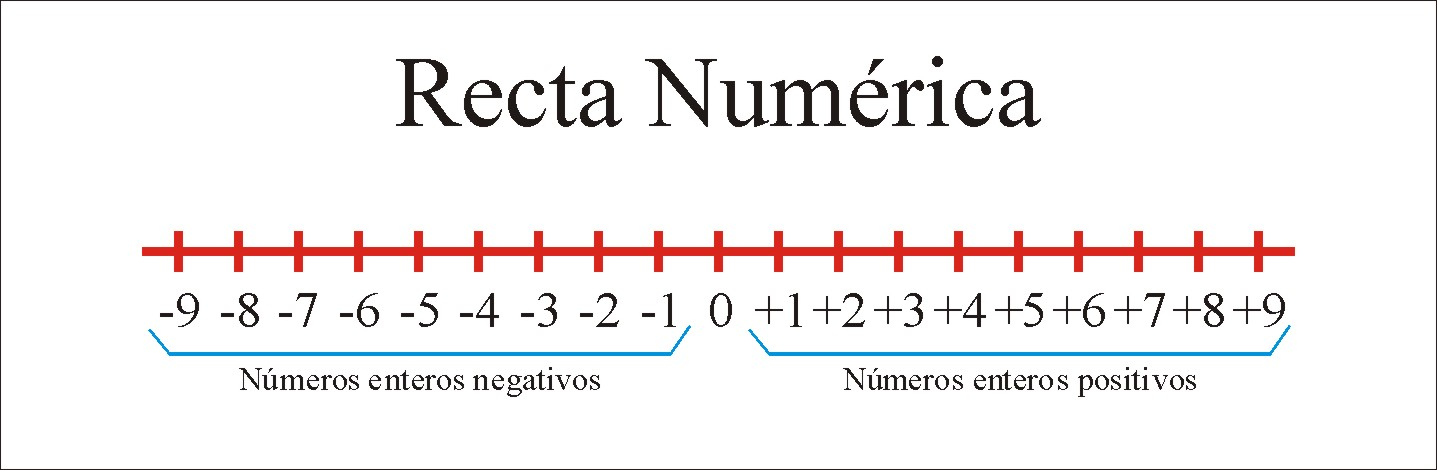
Para representar los números enteros nos fijamos si:

*Si son positivos se sitúan a la derecha  *Si son negativos se sitúan a la izquierda

VALOR ABSOLUTO DE UN NÚMERO ENTERO:

https://www.youtube.com/watch?v=AhQ_DKXp4-g

OPUESTO DE UN NÚMERO ENTERO:

El opuesto de un número es otro número entero con el mismo valor absoluto pero con distinto signo.

Ejemplo: Número 5 -8 -6 3

Opuesto -5 8 6 -3

Ejemplo 1

Un pescador está sentado en un bote a 2 pies sobre la superficie de un lago. El anzuelo de su caña de pescar está flotando 6 pies bajo la superficie. Utiliza los números enteros para representar la posición del pescador y el anzuelo.

Piensa en una recta numérica vertical.

La superficie del lago puede ser representada por el entero 0.

Un pescador está sentado a 2 pies sobre la superficie del lago, por lo que puedes representarlo como +2 o 2.

El anzuelo está flotando 6 pies bajo la superficie, así que puedes representarlo como -6.

EJEMPLO 2

El señor Marsh invirtió en el mercado de valores y perdió $45 el día anterior. La señora Barragán también invirtió en el mercado de valores, pero su inversión tuvo una ganancia de $20 el día anterior. Representa estas situaciones con números enteros.

Piensa en una recta numérica desde -$50 hasta $50. El $0 no representa ni una ganancia ni una pérdida de inversión.

Utiliza un entero negativo para representar una pérdida. El señor Barragán perdió $45 en su inversión, por lo que puede ser representado como -$45

Utiliza un entero positivo para representar una ganancia. La inversión de la señora Marsh tuvo una ganancia de $20. Ésta puede ser representada como +20 o $20, ya que los enteros positivos se pueden escribir con el signo positivo (+) o sin éste.

EJEMPLO 3

La temperatura en el exterior de un centro de esquí era de 3∘F$\begin{array}{r}{3}^{\circ }F\end{array}$ bajo 0∘F$\begin{array}{r}{0}^{\circ }F\end{array}$ . Expresa esa temperatura como un entero.

Para escribir la temperatura como un número entero, tenemos que considerar el termómetro. Un termómetro es una recta numérica vertical. Encuentra la marca para 0∘F$\begin{array}{r}{0}^{\circ }F\end{array}$ en este termómetro y, con tu dedo, cuenta 3∘F$\begin{array}{r}{3}^{\circ }F\end{array}$ bajo esa marca.

Tu dedo señalará el −3∘F$\begin{array}{r}-3^{\circ }F\end{array}$ . Así es como la temperatura 3∘F$\begin{array}{r}{3}^{\circ }F\end{array}$ bajo 0∘F$\begin{array}{r}{0}^{\circ }F\end{array}$ puede ser expresada como un entero. Utilizamos esta medición todo el tiempo. Piensa en el invierno o en el verano. Cuando hace mucho calor o mucho frío, los enteros nos ayudan a comprender qué tan caluroso o qué tan frío está.

Con los enteros se pueden representar muchas situaciones de la vida cotidiana, tales como:

• Aumento y disminución de la temperatura.
• Ganancias y pérdidas de dinero.
• Ubicaciones sobre el mar y bajo el mar.

TALLER DE COMPETENCIAS

A. Escribe cada ejercicio como un número entero.

1. 10 grados bajo cero.

2. Piso 5

3. Una pérdida de $20.000

4. 35 pies bajo la superficie.

5. 120 pies bajo el nivel del mar

6. Una altitud de 15.000 pies

B. Utiliza dos enteros y el signo de una operación para representar cada situación.

7. Una pérdida de 20 y una ganancia de 15.

8. Una ganancia de 15 y una pérdida de veinte.

9. Una ganancia de 20 y una ganancia de 35.

10. Una pérdida de 19 y otra pérdida de 30.

11. Una altitud de 30.000 pies y otra altitud de 15.000 pies.

12. Una pérdida de 15.000 pies y otra pérdida de 12.000 pies.

13. Una profundidad de 60 pies y una parada para descansar a 15 pies bajo la superficie del agua.

14. Una profundidad de 15 pies y luego otro descenso de 20 pies bajo la superficie del agua.

15. Un senderista subió 1500 pies y luego caminó otros 1000 pies.

Copia y Resuelve en el cuaderno.

En la próxima clase se socializa el Taller

BENDICIONES.